Как найти радиус окружности – руководство, которое осилит даже «чайник»

Основные методы нахождения радиуса 

Через площадь круга 

• Делим площадь круга на число Пи 
• Находим корень из результата 

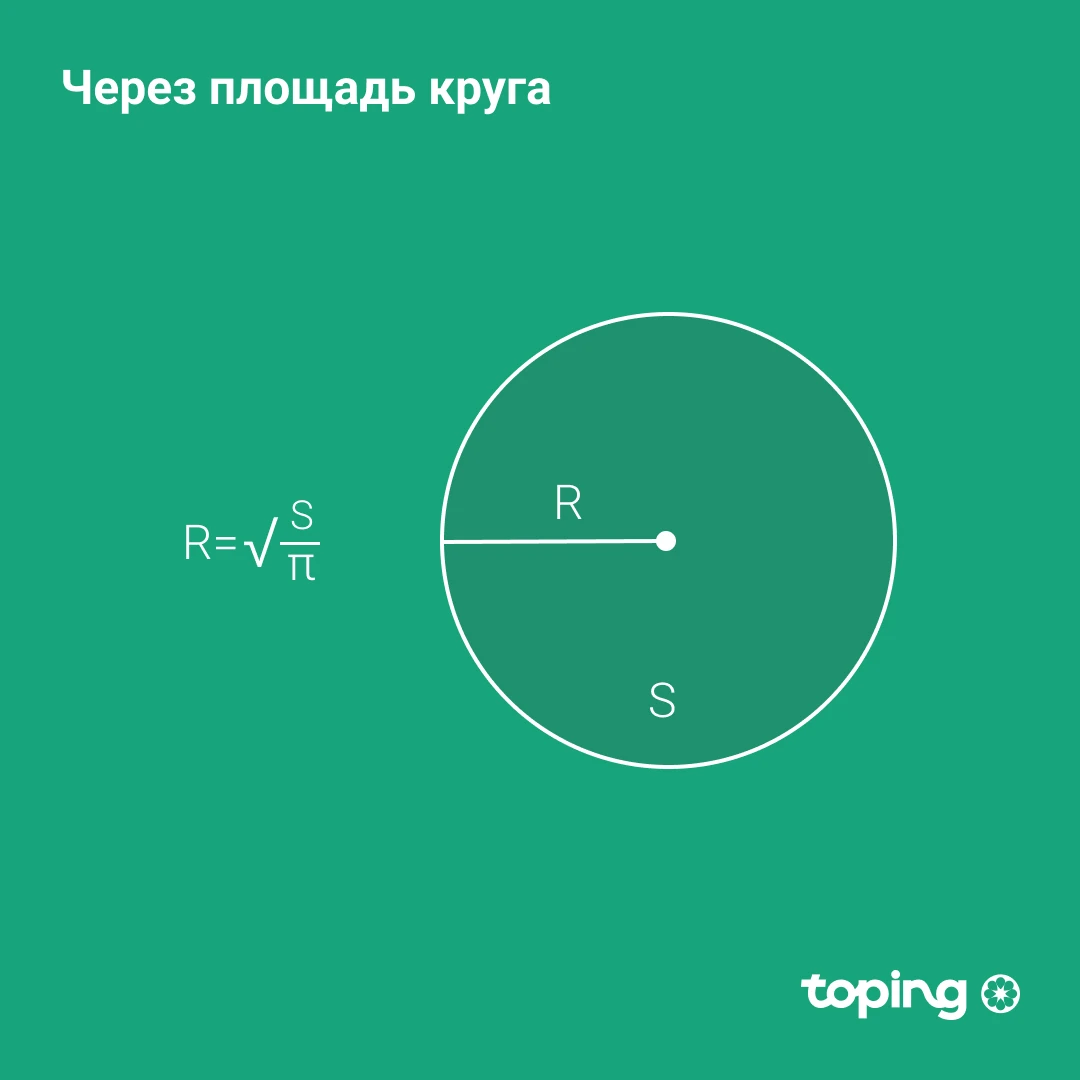
Помним, что R — искомый радиус окружности. S — площадь круга (круг это плоскость внутри окружности. А числом пи называют константу = 3,14.

Через длину окружности 

• Умножаем число пи на 2  
• Теперь делим число окружности с полученным результатом

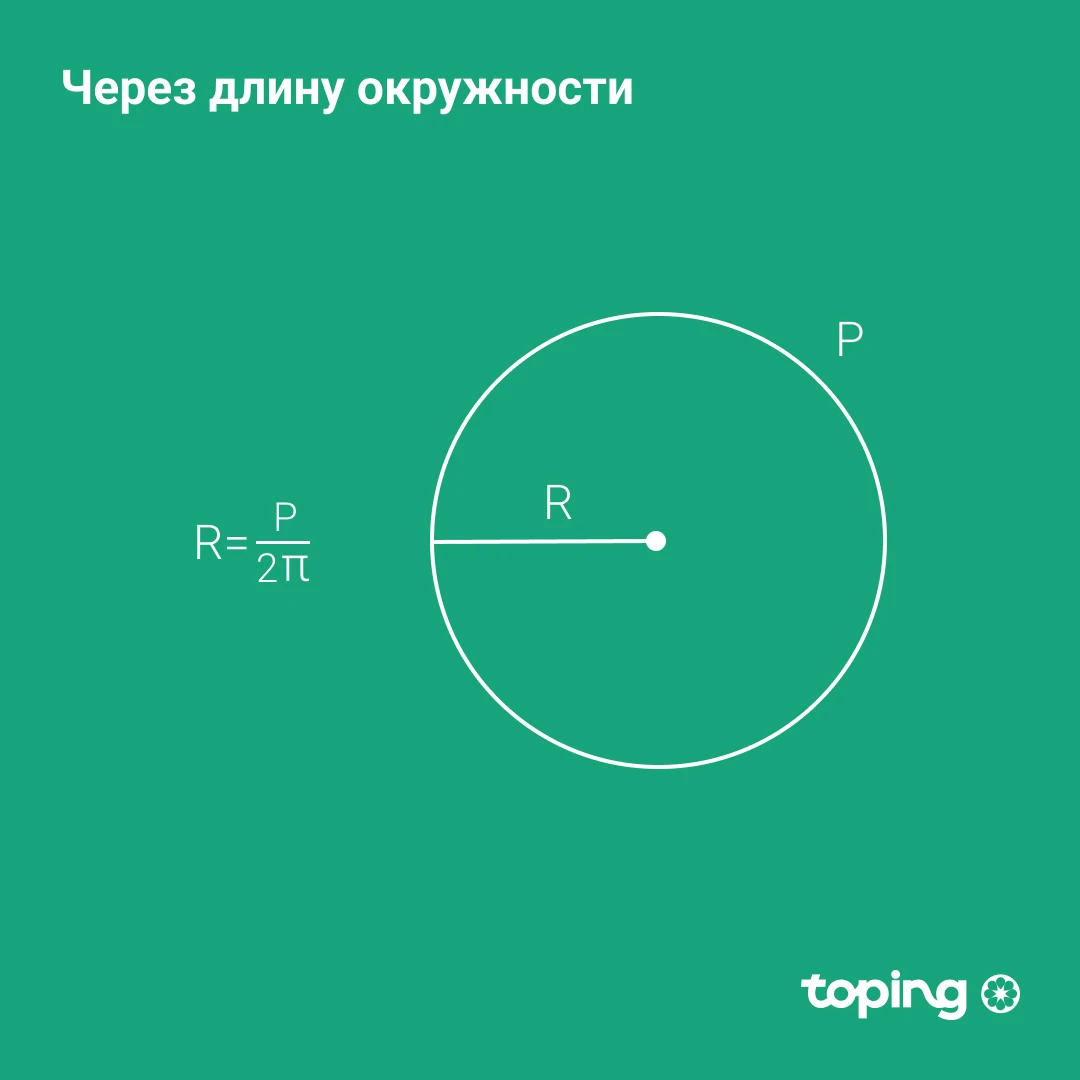
Помним, что R — искомый радиус окружности. P — длина (или периметр) окружности А пи – все еще константа. Она равна 3,14.

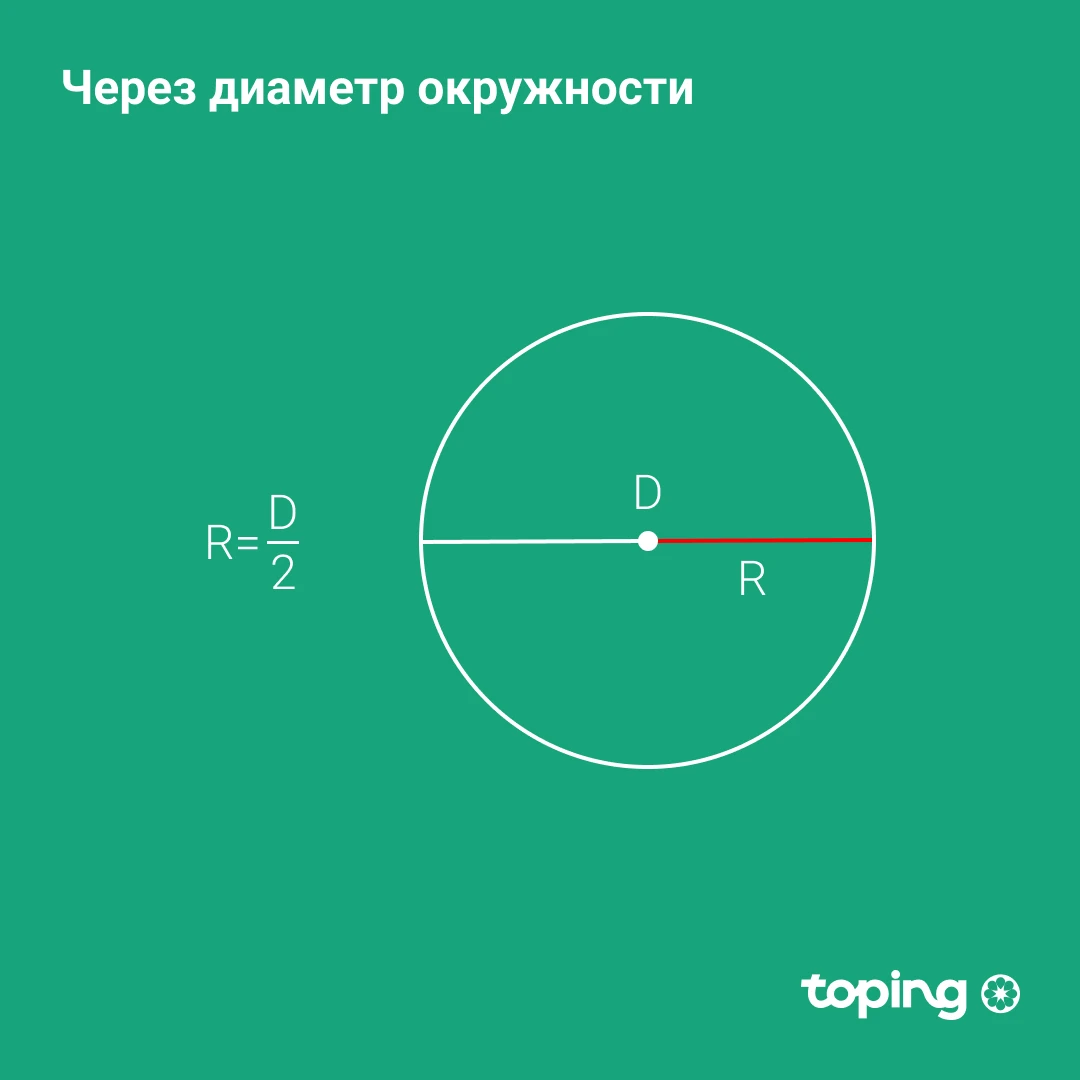
Через диаметр окружности 

Для тех, кто забыл (или не знал первоначально), радиус приравнивают к половине диаметра. Исходя из этого: если диаметр (D) уже известен, то просто разделите его на два.

Дополнительные методы нахождения радиуса

Через диагональ вписанного прямоугольника

В этом случае диагональю называют диаметр окружности, в которую вписан прямоугольник. Диаметр в два раза больше радиуса. Значит достаточно разделить диагональ на 2. 

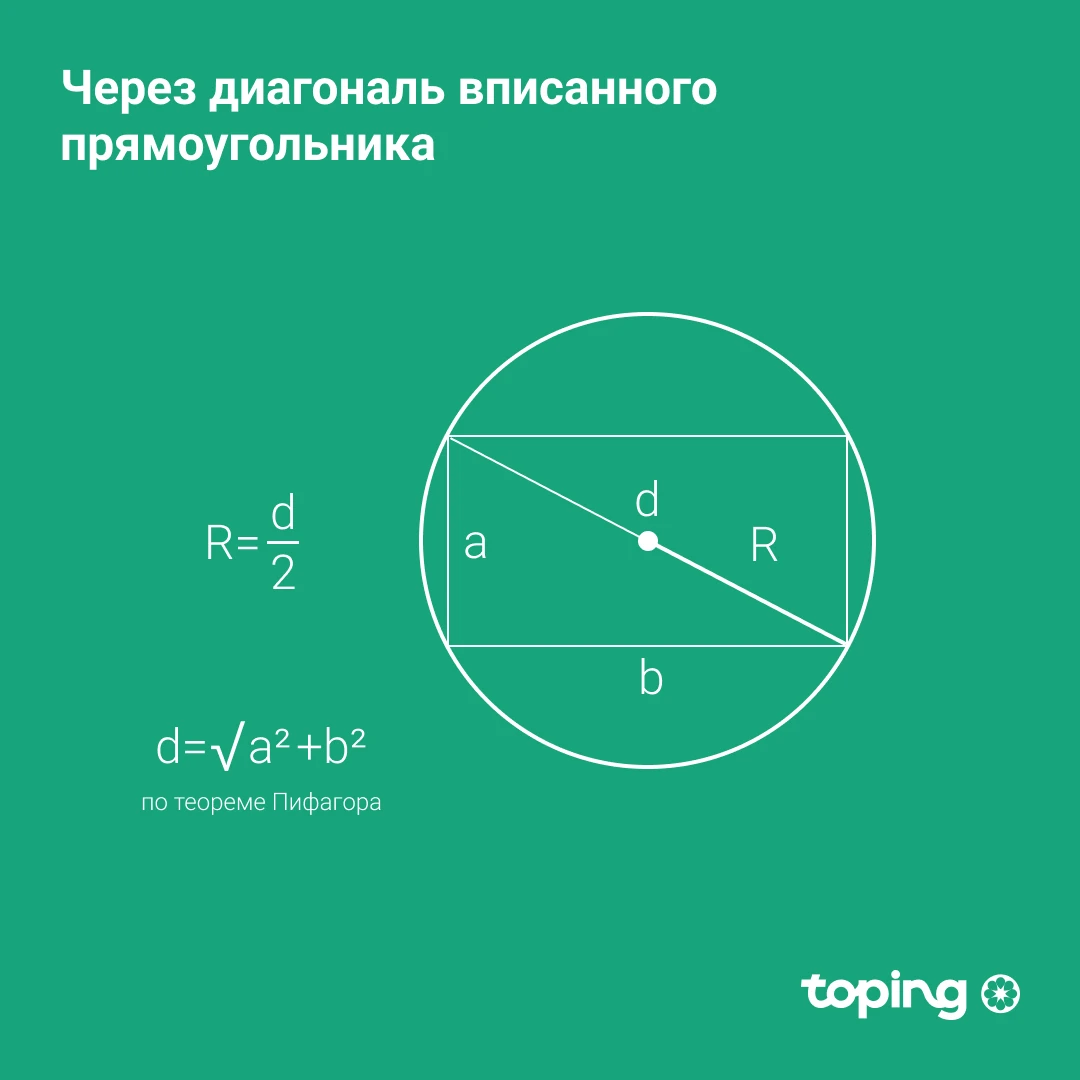
R — искомый радиус окружности. d — диагональ прямоугольника (делит фигуру на 2 прямоугольных треугольника и является их гипотенузой — стороной напротив прямого угла). И если диагональ неизвестна, ее можно отыскать через соседние стороны прямоугольника. В этом поможет теорема Пифагора. 

a и b — это стороны прямоугольника.

Через сторону описанного квадрата

Сторона этого квадрата приравнивается к диаметру окружности. Он, как известно, равен 2 радиусам. А значит делим сторону квадрата на 2.

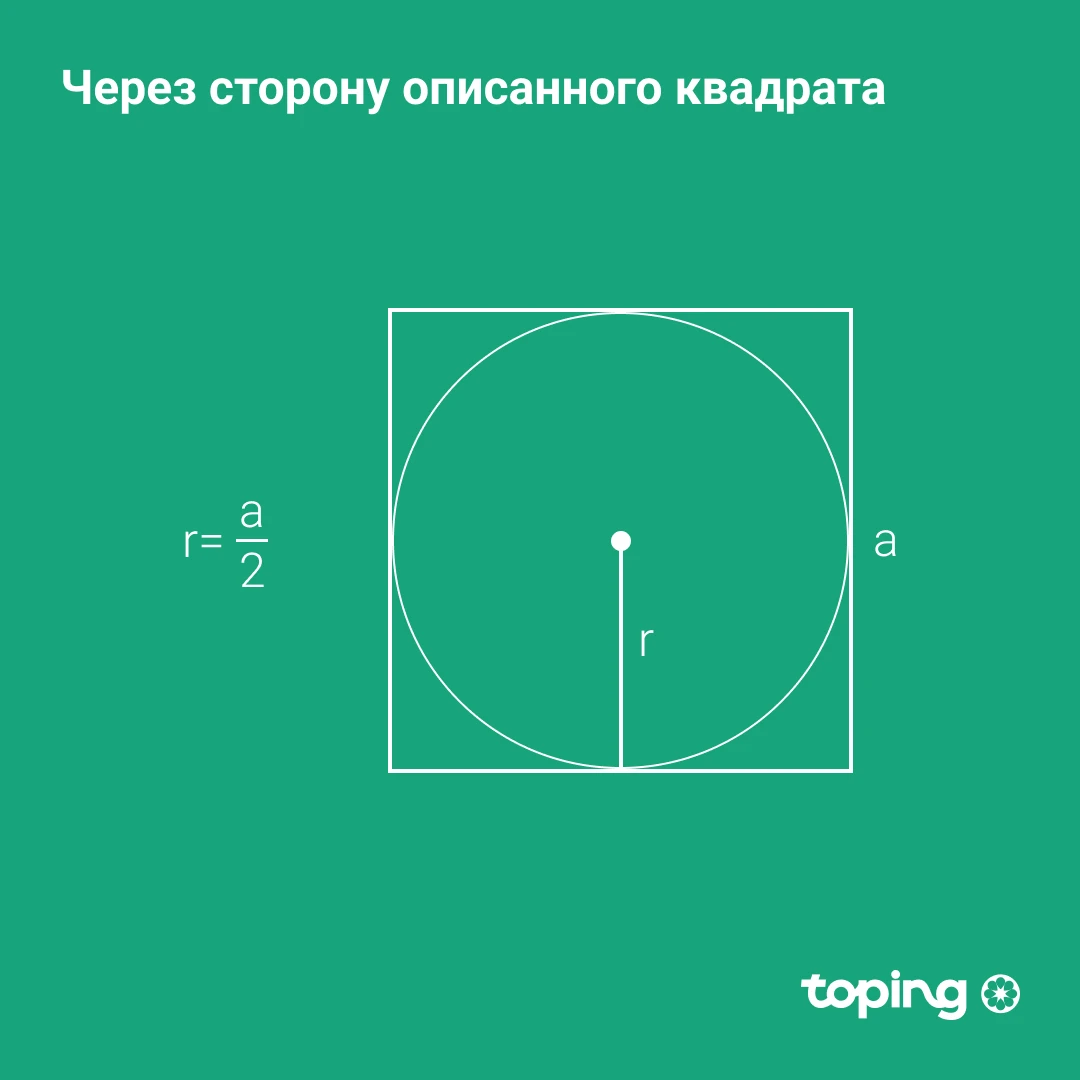
r — радиус окружности. a — сторона квадрата.

Через стороны и площадь вписанного треугольника

• Умножаем три стороны треугольника
• Полученный результат делим на 4 его площади 

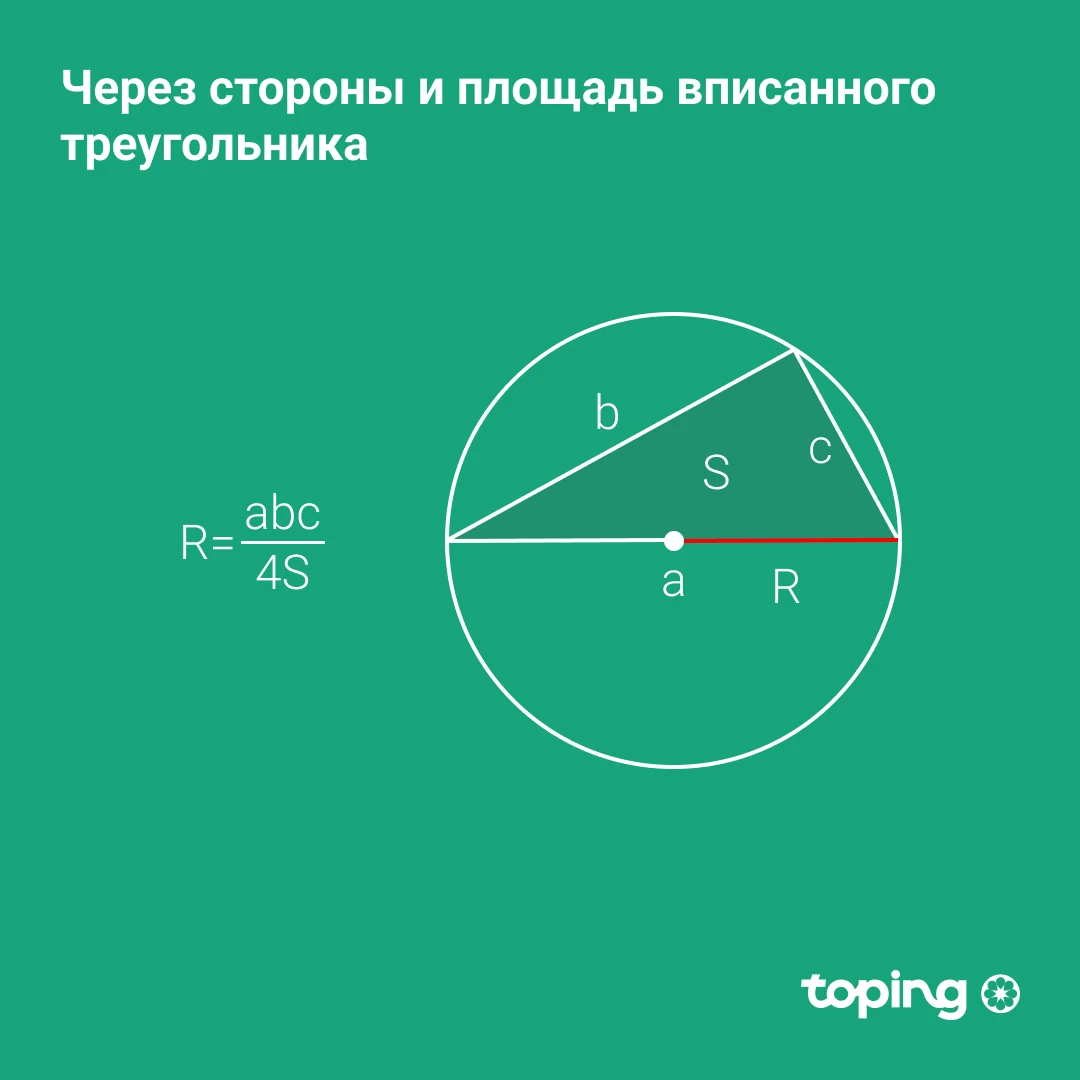
R — радиус окружности. a, b, с — стороны треугольника. S — площадь треугольника

Через площадь и полупериметр описанного треугольника

Делим площадь описанного треугольника на его полупериметр.

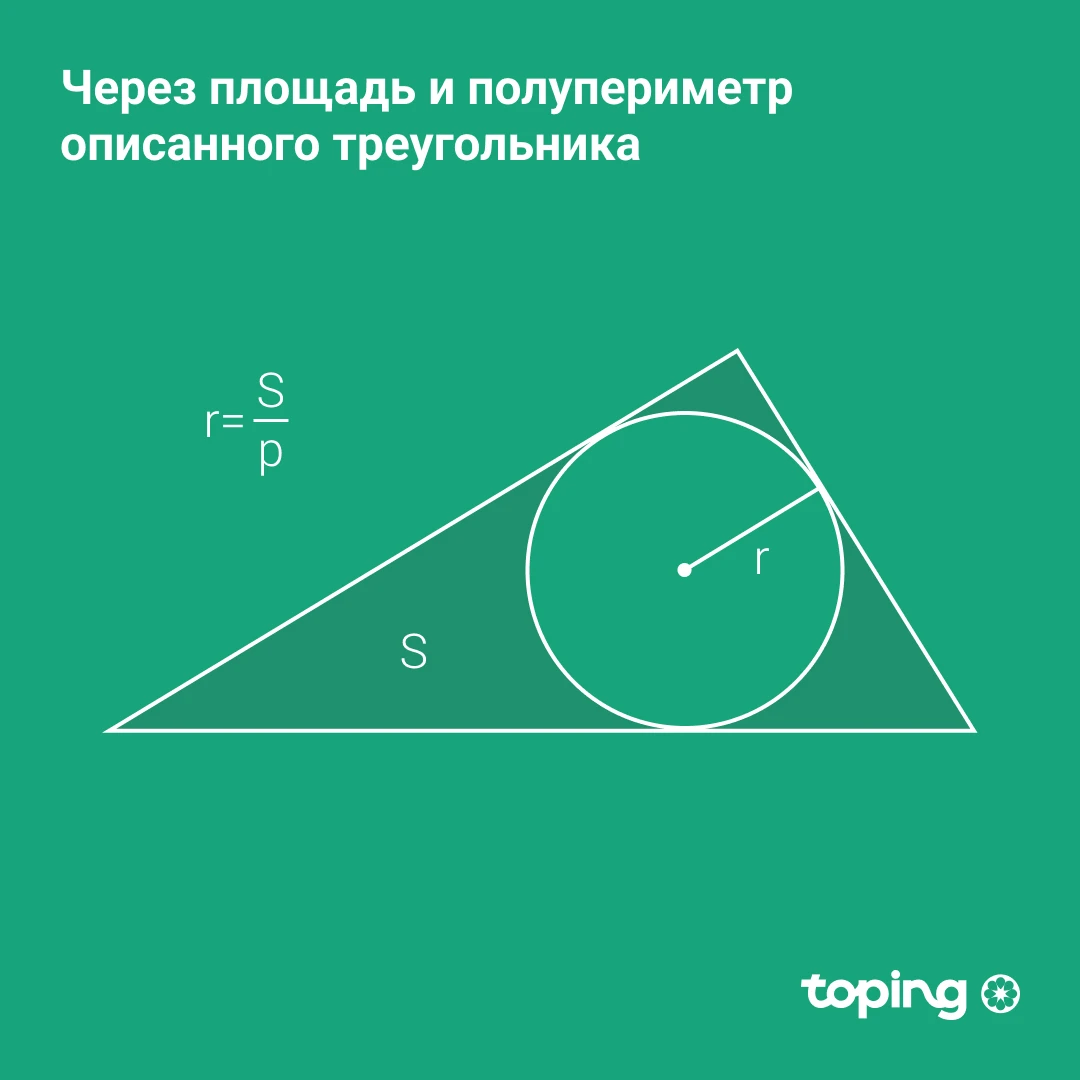
r — радиус окружности. S — площадь треугольника. p — полупериметр треугольника

Через площадь сектора и его центральный угол 

• Умножаем площадь сектора на 360 градусов. 
• Делим результат на произведение центрального угла и пи. 
• Находим корень из полученного числа. 

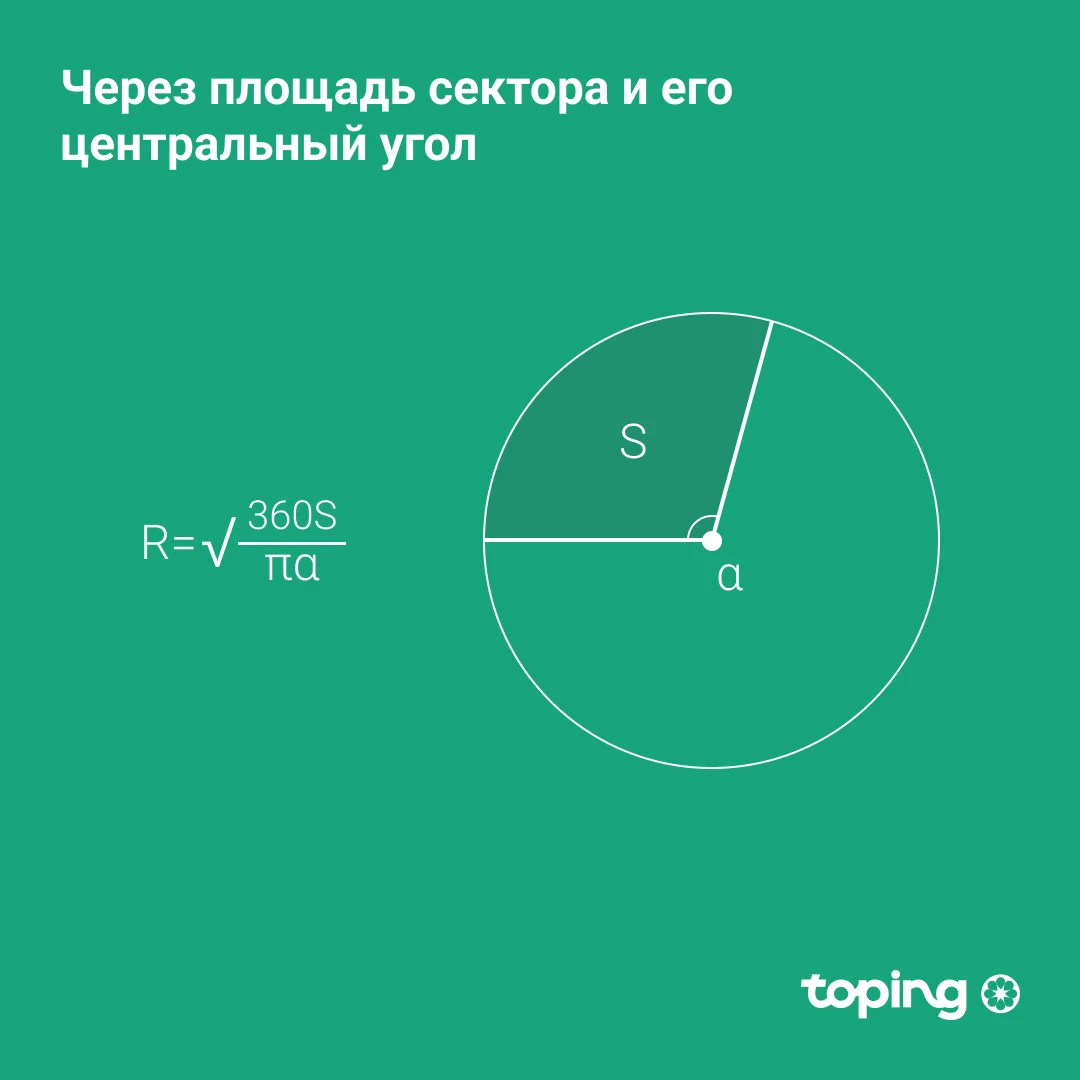
R — радиус окружности. S — площадь сектора круга. α — центральный угол. Пи — константа = 3,14. 

Через сторону вписанного правильного многоугольника 

• Делим 180 градусов на стороны многоугольника (количество). 
• Находим синус полученного числа. 
• Умножаем полученный результат на 2. 
• Делим сторону многоугольника на результат всех вышеописанных действий 

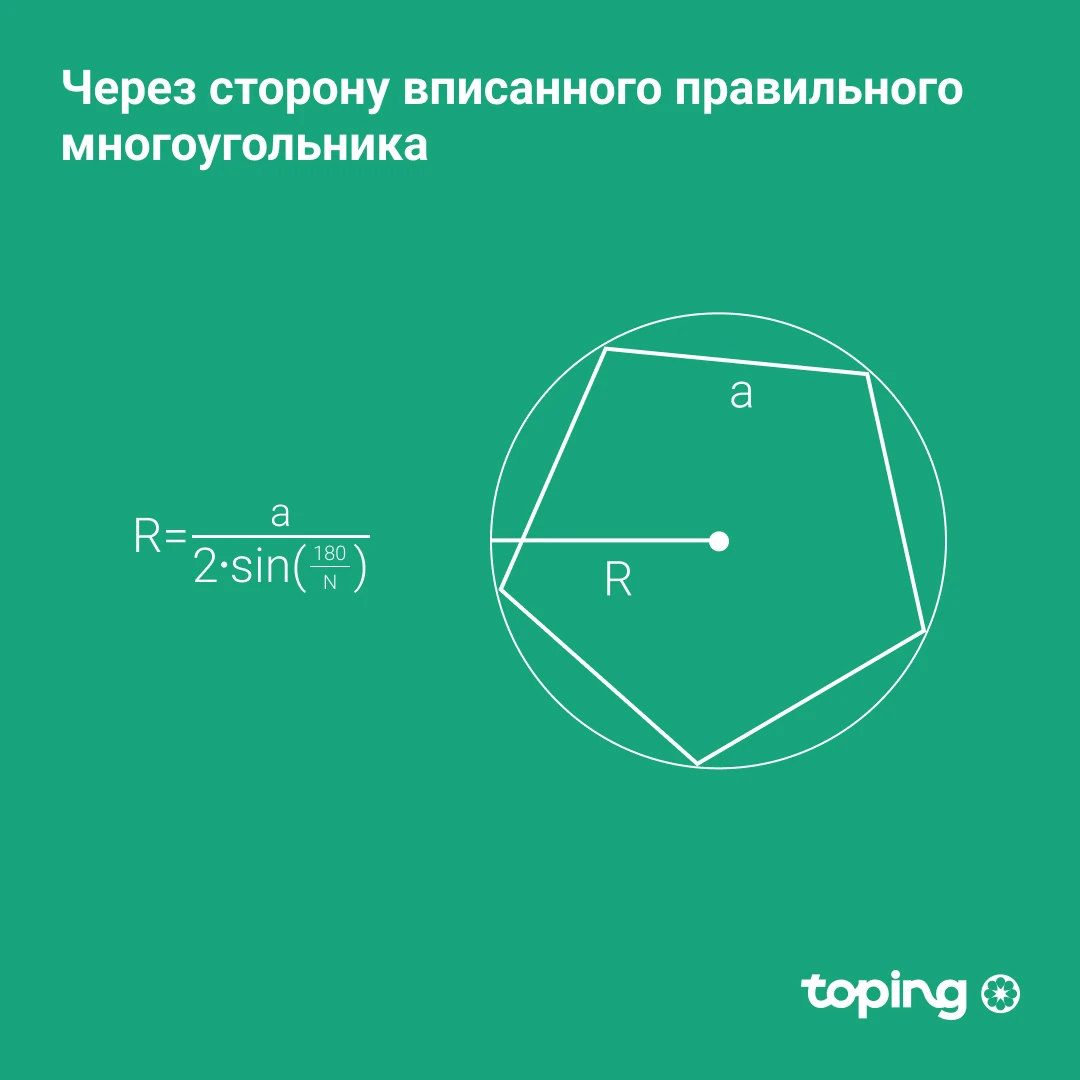
Помните, что в классическом многоугольнике все стороны равны. N это количество сторон многоугольника. 

Примеры и задачи 

Как рассчитать радиус через площадь круга 

Как рассчитать радиус через длину окружности 

Как рассчитать радиус через диаметр окружности

Часто спрашивают 

Как найти радиус, если известна только длина окружности? 

Если у нас есть длина окружности, то радиус можно найти с помощью известной формулы, которая связывает длину окружности с радиусом: r = L/2п, где L - длина окружности, п = 3,14.

Можно ли найти радиус, если известны только углы вписанного треугольника? 

Знать только углы вписанного треугольника недостаточно для вычисления радиуса окружности. Однако, если имеется дополнительная информация, такая как длина хотя бы одной стороны треугольника или его окруженного треугольника (круга, в который вписан треугольник), то можно использовать тригонометрические формулы и теоремы для расчета. Например, можно использовать формулу для окружности, в которую вписан треугольник, и известную теорему синусов.

Однако, без дополнительных данных (например, длины сторон треугольника), вычислить радиус невозможно только на основании углов.

Какие еще существуют методы нахождения радиуса окружности? 

Существуют различные способы нахождения радиуса окружности, в зависимости от известной информации. Самые распространенные – по площади круга, по диаметру, по длине дуги и центральному углу, используя уравнение окружности, метода геометрического места точек. 

Каждый из этих методов подходит для разных ситуаций, и выбор зависит от того, какая информация есть у вас в голове, и на руках. 

И напоследок, еще топ-7 полезных советов

1. Определяйте радиус через известные параметры 
2. Работайте с диаметром 
3. Используйте треугольники 
4. Применяйте геометрические свойства
5. И координатные методы
6. Подходите к задачам правильно – анализируйте 
7. Проверяйте результаты