Қандай қилиб айлана радиусини топиш мумкин – ҳаттоки “чойнак”ни ҳам зифлаштирган қўлланма

Радиусни топишнинг асосий усуллари

Доира юзи орқали

• Доира юзини Пи сонига бўламиз
• Натижадан илдиз топамиз

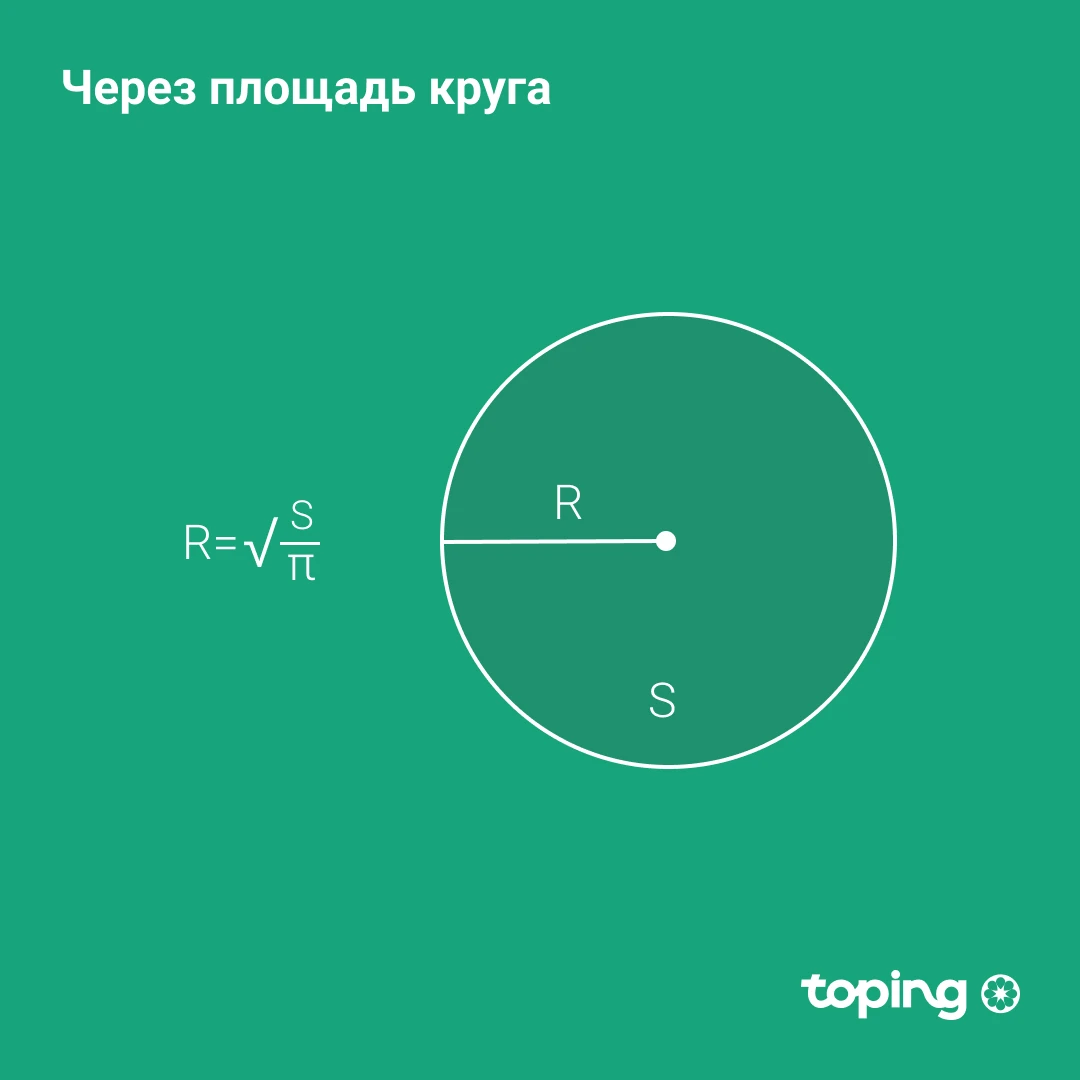
Р - айлананинг изланган радиуси эканини эсга оламиз. С - доиранинг юзи (доира - айлана ичидаги текислик. Пи сони эса = 3,14 константи деб аталади.

Айлана узунлиги орқали

• Пи сонини 2 га кўпайтирамиз
• Энди ҳосил бўлган натижа билан айлана сонини бўламиз

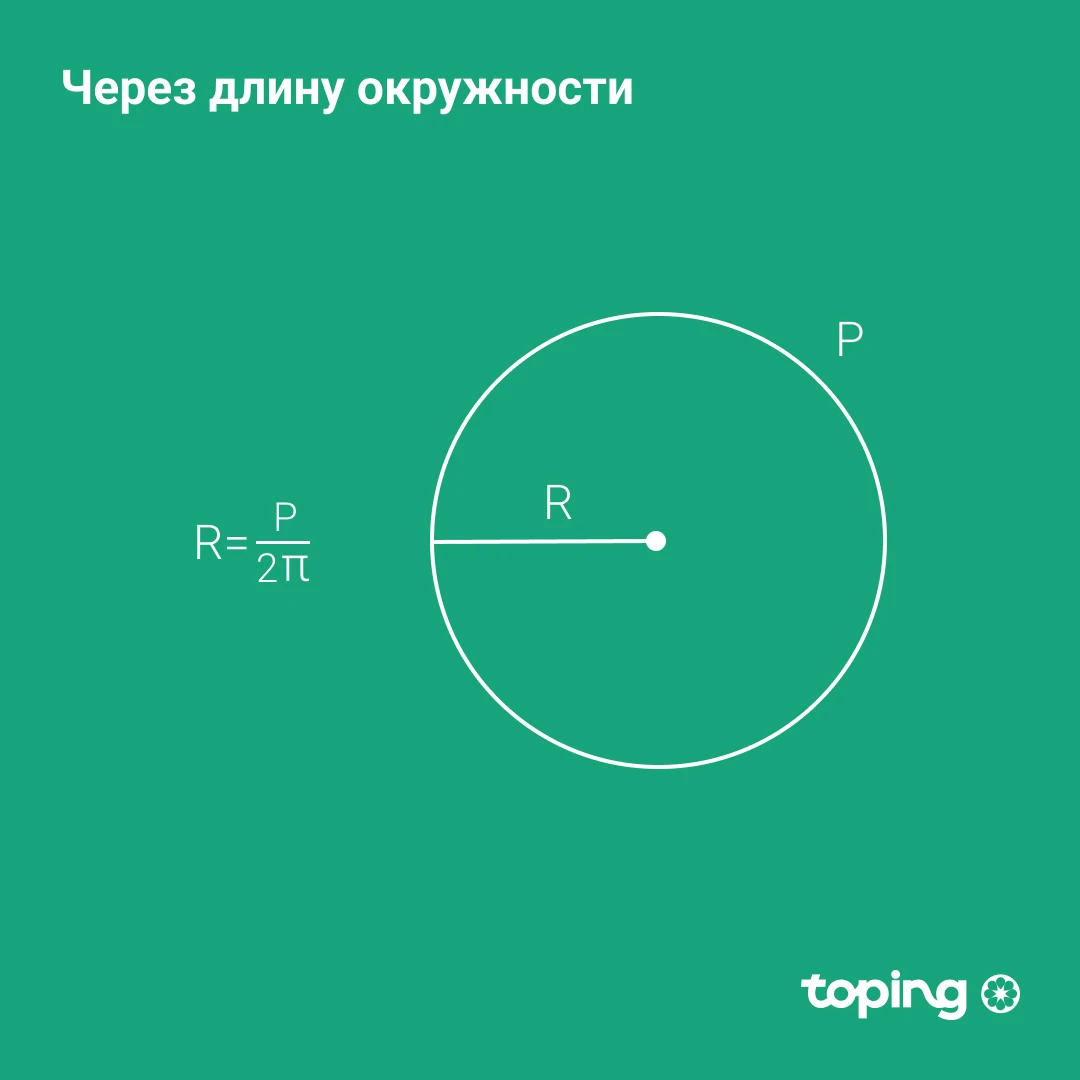
Эсга оламиз, Р - айлананинг изланган радиуси. П - айлананинг узунлиги (ёки периметри), Пи эса - ҳали ҳам ўзгармас. У 3,14 га тенг.

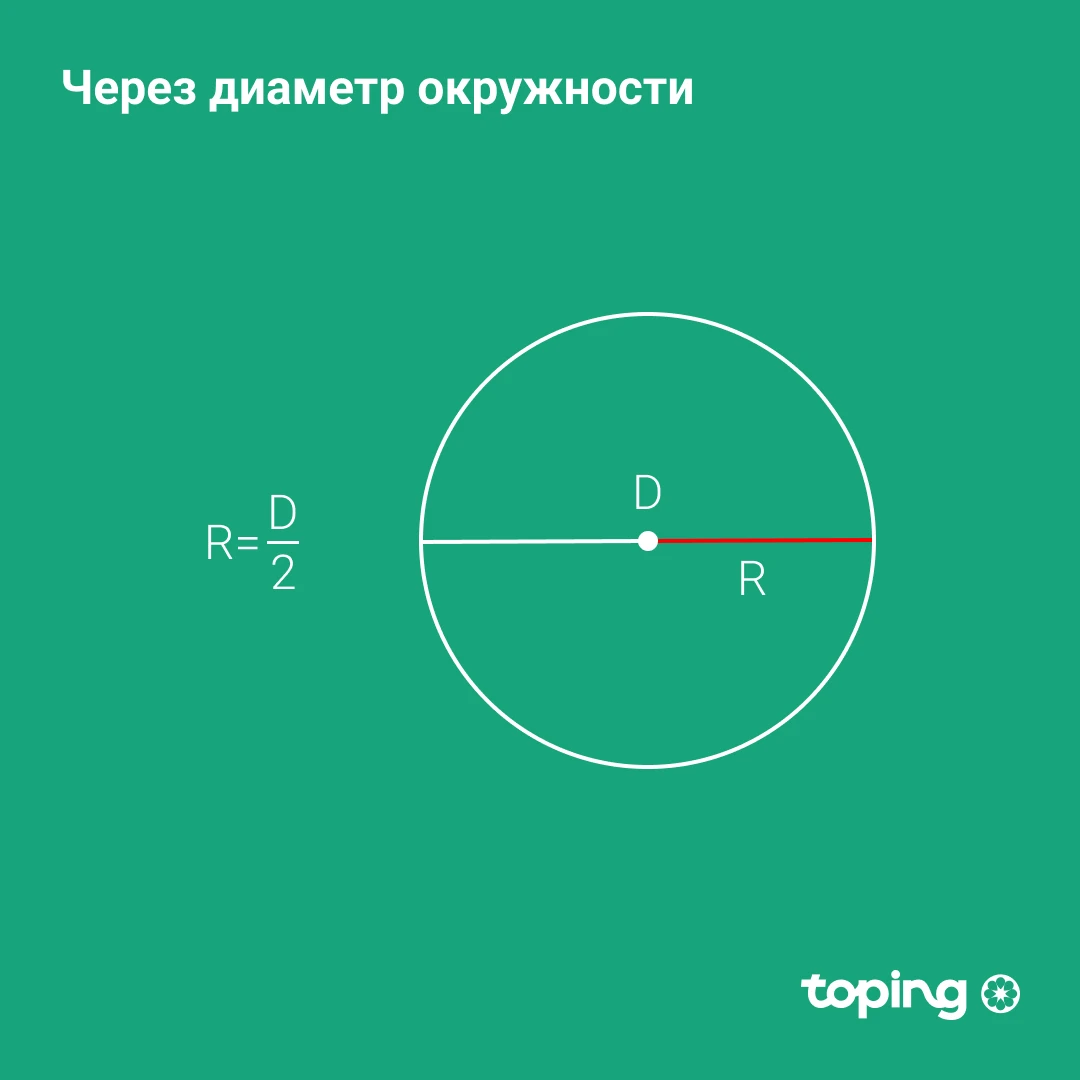
Айлана диаметри орқали

Ёддан кўтарганлар учун (ёки олдиндан билмаганлар учун) радиус диаметрнинг ярмига тенглаштирилади. Шунга кўра: агар диаметр (Д) маълум бўлса, уни шунчаки иккига бўлинг.

Радиусни топишнинг қўшимча усуллари

Ички чизилган тўғри тўртбурчак диагонали орқали

Бундай ҳолатда тўғри тўртбурчак чизилган айлананинг диаметри диагонал дейилади. Диаметр радиусдан икки марта катта. Демак, диагонални 2 га бўлиш етарли.

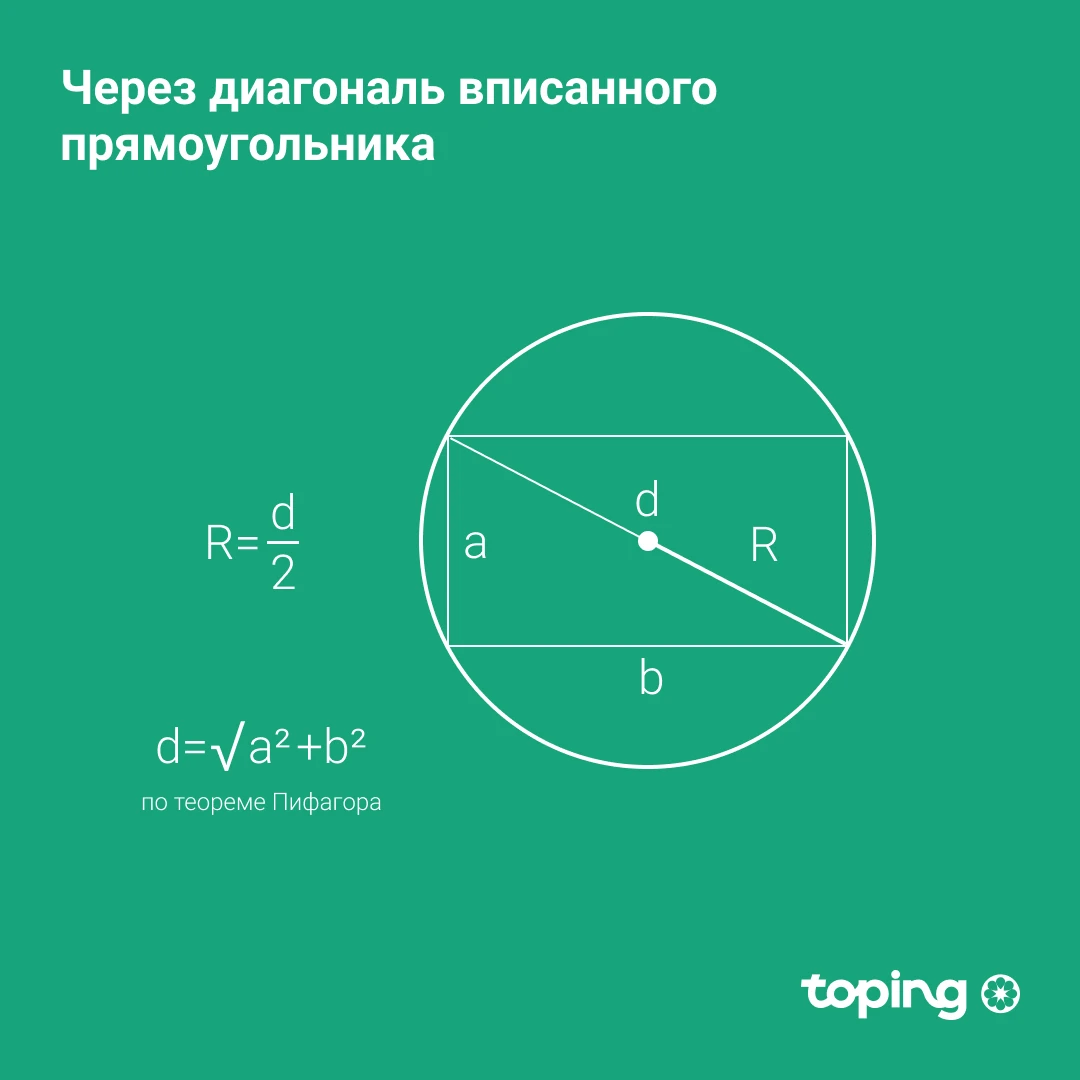
Р - изланган айлана радиуси. д - тўғри тўртбурчак диагонали (шакл 2 та тўғри бурчакли учбурчакка бўлинади ва уларнинг тўғри бурчакнинг қарама-қарши томони - гипотенузаси ҳисобланади). Агар диагонал номаълум бўлса, уни тўғри тўртбурчакнинг қўшни томонлари орқали топиш мумкин. Бунда Пифагор теоремаси ёрдам беради.

Чизилган квадратнинг томони орқали

Бу квадратнинг томони айлана диаметрига тенг. Маълумки, у 2 радиусга тенг. Демак, квадрат томонини 2 га бўламиз.

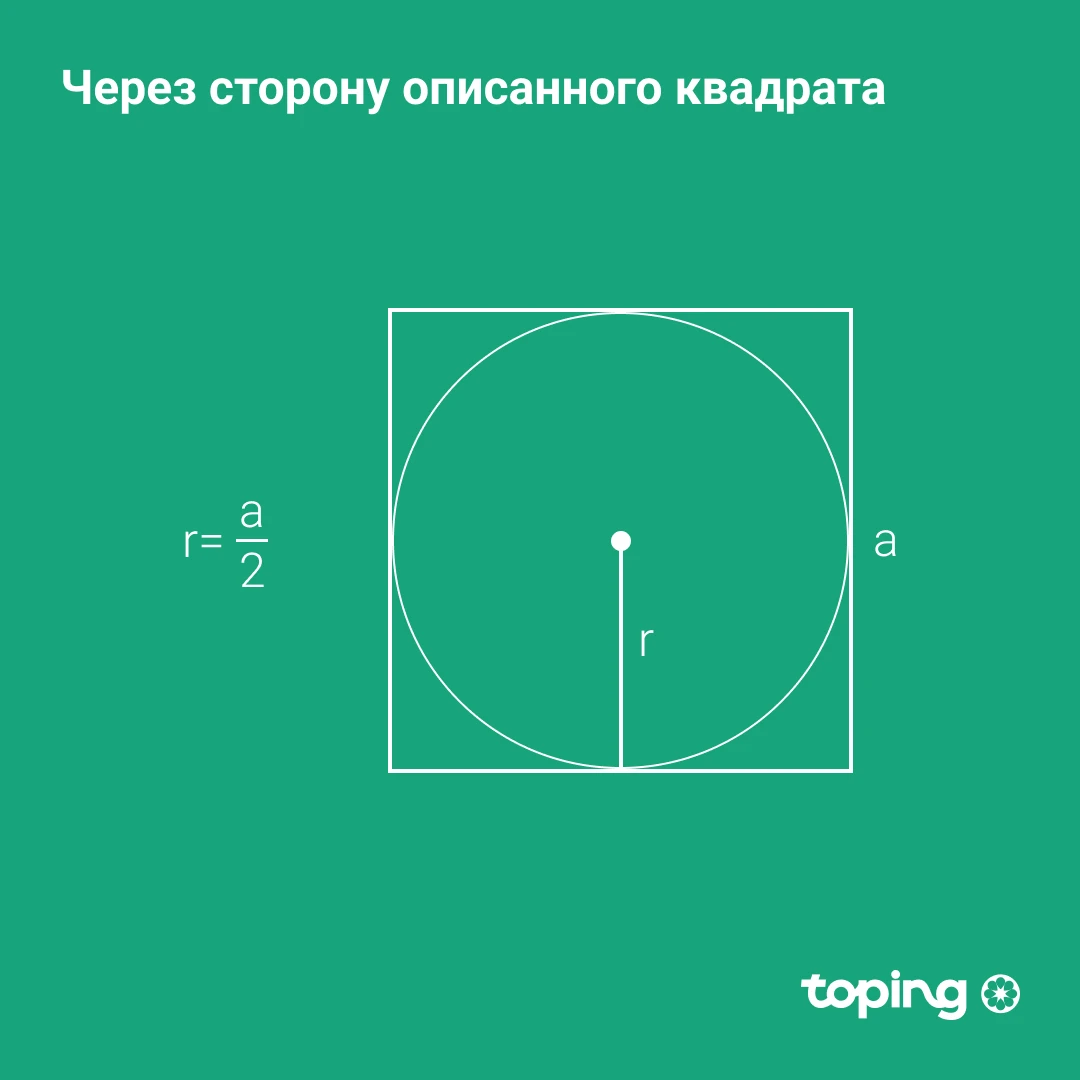
р - айлана радиуси. а - квадрат томони.

Ички чизилган учбурчакнинг томонлари ва юзи орқали

• Учбурчакнинг уч томонини кўпайтирамиз
• Олинган натижани унинг 4 та юзига бўламиз

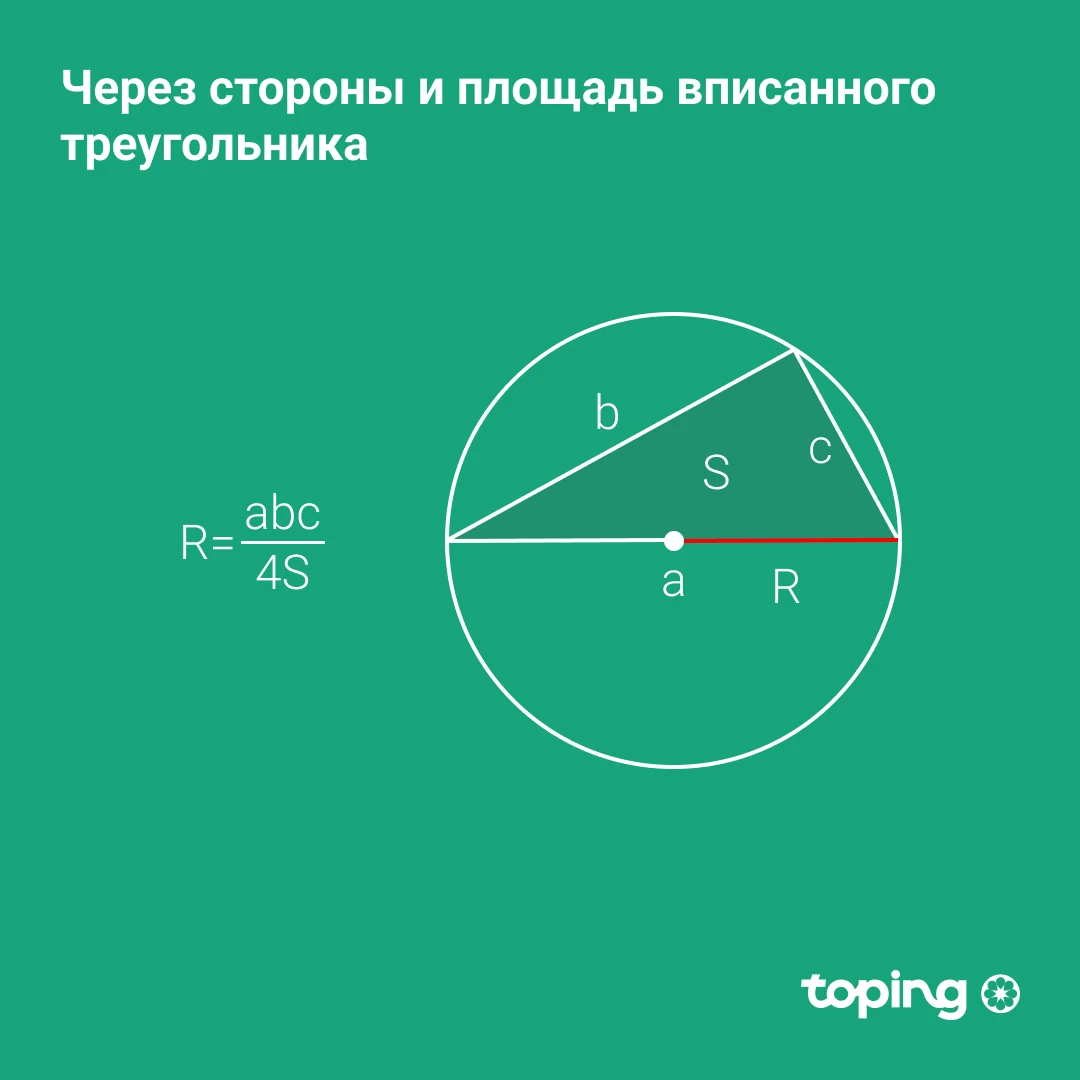
Р - айлана радиуси. а, б, c - учбурчакнинг томонлари. С - учбурчак юзи

Ташқи чизилган учбурчакнинг юзи ва ярим периметри орқали

р - айлана радиуси. С - учбурчакнинг юзи. п - учбурчакнинг ярим периметри

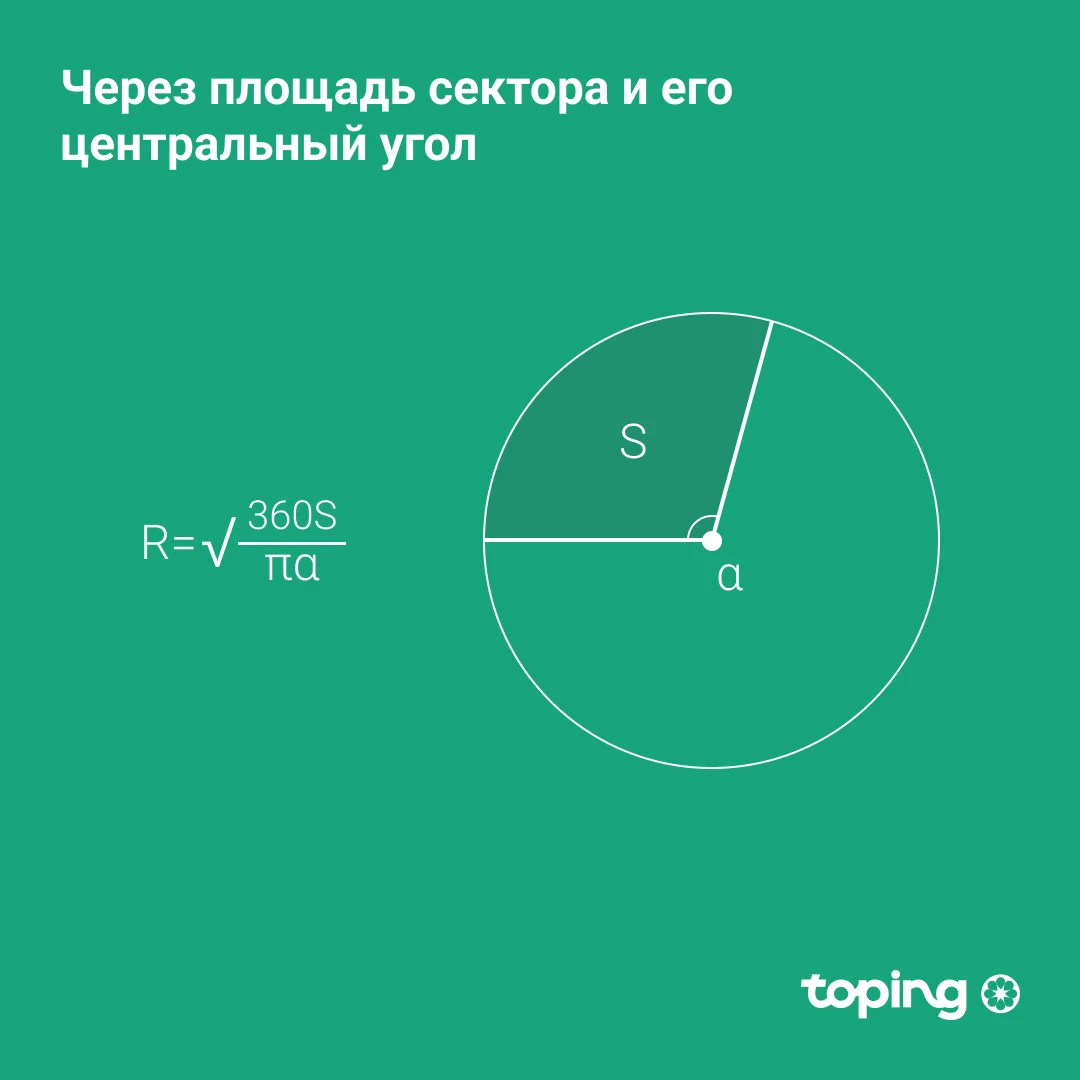
• Сектор майдони ва унинг марказий бурчаги орқали
• Сектор юзини 360 градусга кўпайтирамиз
• Натижани марказий бурчак ва Пи нинг кўпайтмасига бўламиз
• Ҳосил бўлган соннинг илдизини топамиз.

Р - айлана радиуси. С - айлана секторининг юзи. α - марказий бурчак. Пи - константа = 3,14.

Ички чизилган мунтазам кўпбурчакнинг томони орқали

• 180 градусни кўпбурчак томонларига бўламиз (сони)
• Ҳосил бўлган соннинг синусини топамиз
• Олинган натижани 2 га кўпайтирамиз.
• Кўпбурчакнинг томонини юқорида қайд этилган барча амаллар натижасига бўламиз

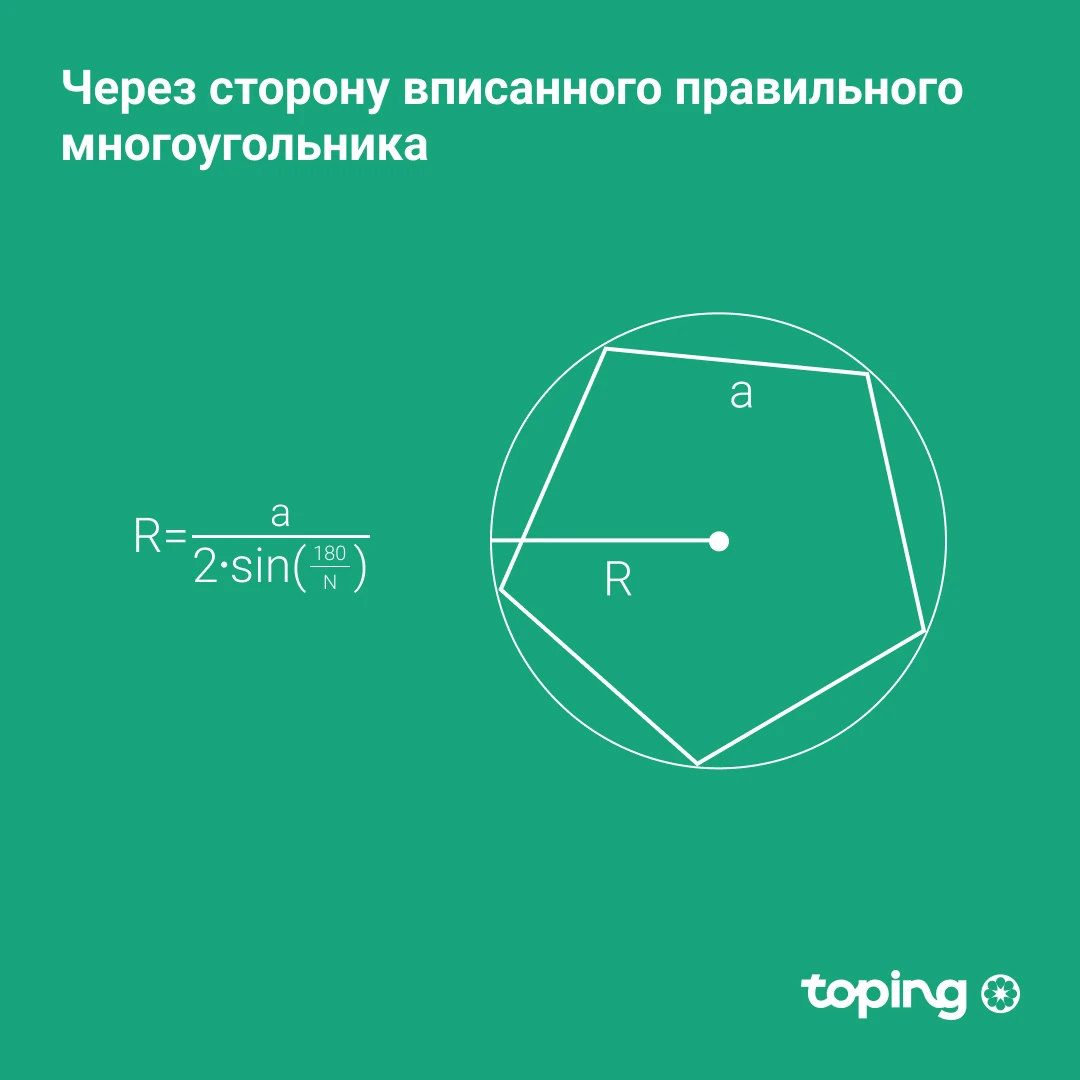
Классик кўпбурчакнинг барча томонлари тенг эканини эсга олинг. Н – бу кўпбурчак томонларининг сони.

Мисоллар ва масалалар

Радиус доиранинг юзи орқали қандай ҳисобланади

Радиус айлананинг узунлиги орқали қандай ҳисобланади

Радиус айлананинг диаметриc орқали қандай ҳисобланади

Кўпинча сўрашади

Агар айлананинг фақат узунлиги маълум бўлса, радиус қандай топилади?

Агар бизда айлана узунлиги бўлса, у ҳолда радиусни айлана узунлигини радиус билан боғлайдиган маълум бир формула ёрдамида топиш мумкин: р = Л/2л, бу ерда Л - айлана узунлиги, Пи = 3,14.

Ички чизилган учбурчакнинг фақат бурчаклари маълум бўлса, унинг радиусини топиш мумкинми?

Ички чизилган учбурчакнинг фақат бурчакларини билиш айлананинг радиусини ҳисоблаш учун етарли емас. Бироқ, агар учбурчакнинг ҳеч бўлмаганда бир томони ёки унинг атрофидаги учбурчакнинг (учбурчакка ички чизилган доиранинг) узунлиги каби қўшимча маълумотлар мавжуд бўлса, ҳисоблаш учун тригонометрик формулалар ва теоремалардан фойдаланиш мумкин. Масалан, ичига учбурчак ички чизилган айлана учун формула ва синуслар теоремасидан фойдаланиш мумкин.

Бироқ қўшимча маълумотларсиз (масалан, учбурчак томонларининг узунликлари) радиусни фақат бурчаклар асосида ҳисоблаб бўлмайди.

Айлана радиусини топишнинг яна қандай усуллари мавжуд?

Маълум маълумотлардан келиб чиқиб, айлана радиусини топишнинг турли усуллари мавжуд. Э г кенг тарқалганлари - айлана тенгламаси, нуқталарнинг геометрик ўрни усулидан фойдаланиб, доира юзи, диаметри, ёйи узунлиги ва марказий бурчаги бўйича.

Ушбу усулларнинг ҳар бири турли вазиятлар учун мос келади ва танлаш сизда ва қўлингизда қандай маълумот борлигига боғлиқ.

Ва ниҳоят, яна топ-7 та фойдали маслаҳатлар

1.      Маълум параметрлар орқали радиусни аниқланг

2.      Диаметр билан ишланг

3.      Учбурчаклардан фойдаланинг

4.      Геометрик хоссаларни қўлланг

5.      Координата усуллари

6.      Масалаларга тўғри ёндашинг - таҳлил қилинг

7.      Натижаларни текшириб кўринг